 1
11.Backgrounds of Deep Candidates Generation in recommendation
In this post, we will talk about some real-world applications of deep candidates generation (vector-retrieval) models in the matching stage of recommendation scenario. Commercial recommendation system will recommend tens of millions of items to each user. And the recommendation process usually consists of two stages: The first stage is the candidate generation(matching) stage, a few hundred candidates are selected from the pool of all candidate items. The second stage is the ranking stage in which hundreds of items are ranked and sorted by the ranking score. Then the top rated items are displayed to users.
Why deep candidates generation is important?
Sometimes, only basic information of users (such as gender, age) are available and very few browsing history exist for each user. Using traditional matching techniques will not generate enough candidates for the following ranking stage. Deep candidates generation model (deep-matching) model is adopted to solve this problem. It firstly maps users' features and items' feature to fixed dimensional vector . And then the vector retrieval techniques, such as FAISS, is adopted to find the topK most similar items
to user's embedding vector
. The similarity score is usually the inner-product of two vectors
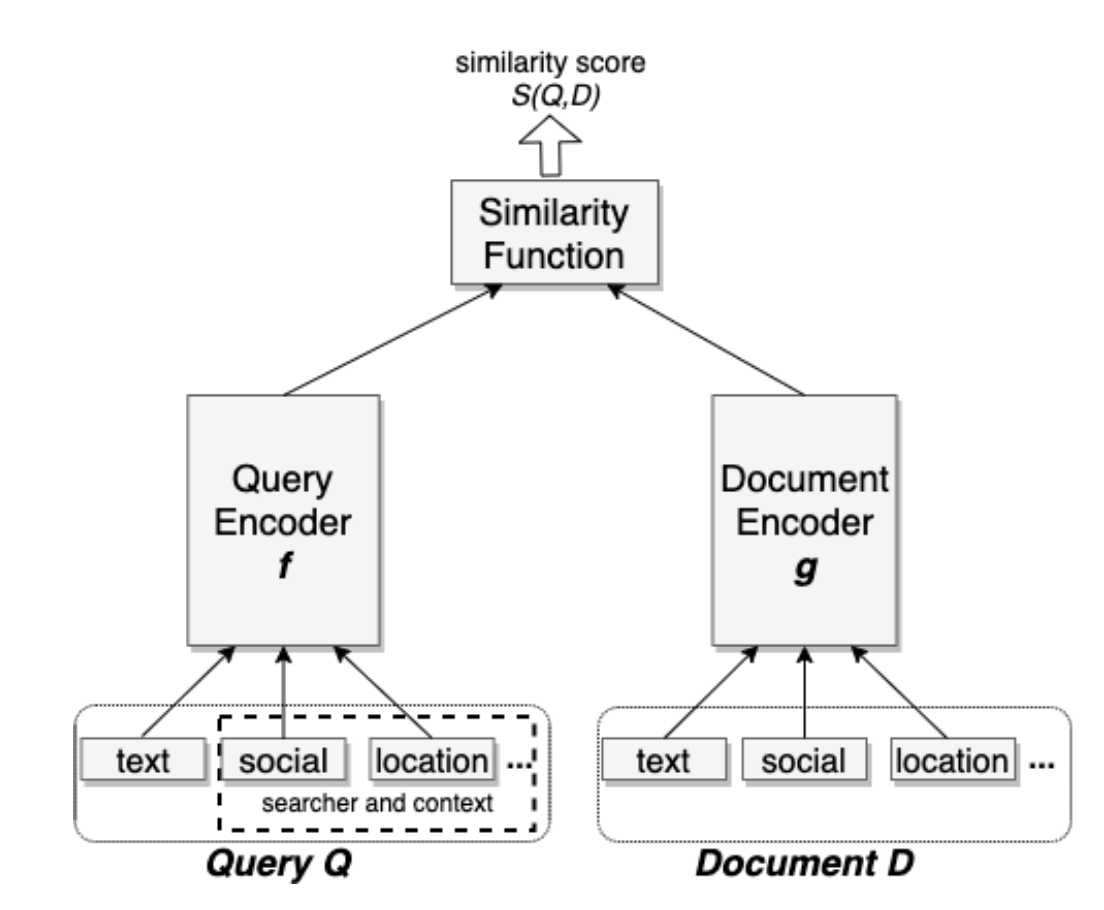
Reference: http://export.arxiv.org/pdf/2006.11632
2.Problem Formulation
Notation
In recommendation scenario, we are recommendation items
to each user.
In the candidate generation problem, users' features and items' features are firstly mapped to a low-dimensional embedding space.
.
are both d-dimensional vectors. There are multiple choices of similarity score, such as cosine similarity, inner-product, etc.
Loss function
We tried to optimize the maximum likelihood function of generating item i from pool of all N candidate items. denotes the i-th candidate item is selected.

3.Training
3.1 Dataset generation and Negative Sampling
In real-world application, negative sampling techniques are adopted to generate negative samples in the candidate generation problem. For each positive sample( user-item clk pair), negative examples are randomly sampled from pool of all candidate items. The distribution of the probability that item i is selected is that,
, which is the occurrence of item i
in positive user-item clicks, divided by count of total positive user-item clicks.
3.2 Training Loss function
Softmax loss function sometimes is not easily calculated. So sampled-softmax or NCE loss is adopted in real-world application, when item size is very large.