Model-Agnostic Meta-Learning MAML
Tags: #machine learning #meta learningEquation
$$\min_{\theta} \sum_{\mathcal{T}_{i} \sim p(\mathcal{T})} \mathcal{L}_{\mathcal{T}_{i}}(f_{\theta^{'}_{i}}) = \sum_{\mathcal{T}_{i} \sim p(\mathcal{T})} \mathcal{L}_{\mathcal{T}_{i}}(f_{\theta_{i} - \alpha \nabla_{\theta} \mathcal{L}_{\mathcal{T}_{i}} (f_{\theta}) })$$Latex Code
\min_{\theta} \sum_{\mathcal{T}_{i} \sim p(\mathcal{T})} \mathcal{L}_{\mathcal{T}_{i}}(f_{\theta^{'}_{i}}) = \sum_{\mathcal{T}_{i} \sim p(\mathcal{T})} \mathcal{L}_{\mathcal{T}_{i}}(f_{\theta_{i} - \alpha \nabla_{\theta} \mathcal{L}_{\mathcal{T}_{i}} (f_{\theta}) })
Have Fun
Let's Vote for the Most Difficult Equation!
Introduction
1.1 MAML Meta-Objective
Equation
Latex Code
\min_{\theta} \sum_{\mathcal{T}_{i} \sim p(\mathcal{T})} \mathcal{L}_{\mathcal{T}_{i}}(f_{\theta^{'}_{i}}) = \sum_{\mathcal{T}_{i} \sim p(\mathcal{T})} \mathcal{L}_{\mathcal{T}_{i}}(f_{\theta_{i} - \alpha \nabla_{\theta} \mathcal{L}_{\mathcal{T}_{i}} (f_{\theta}) })
Explanation
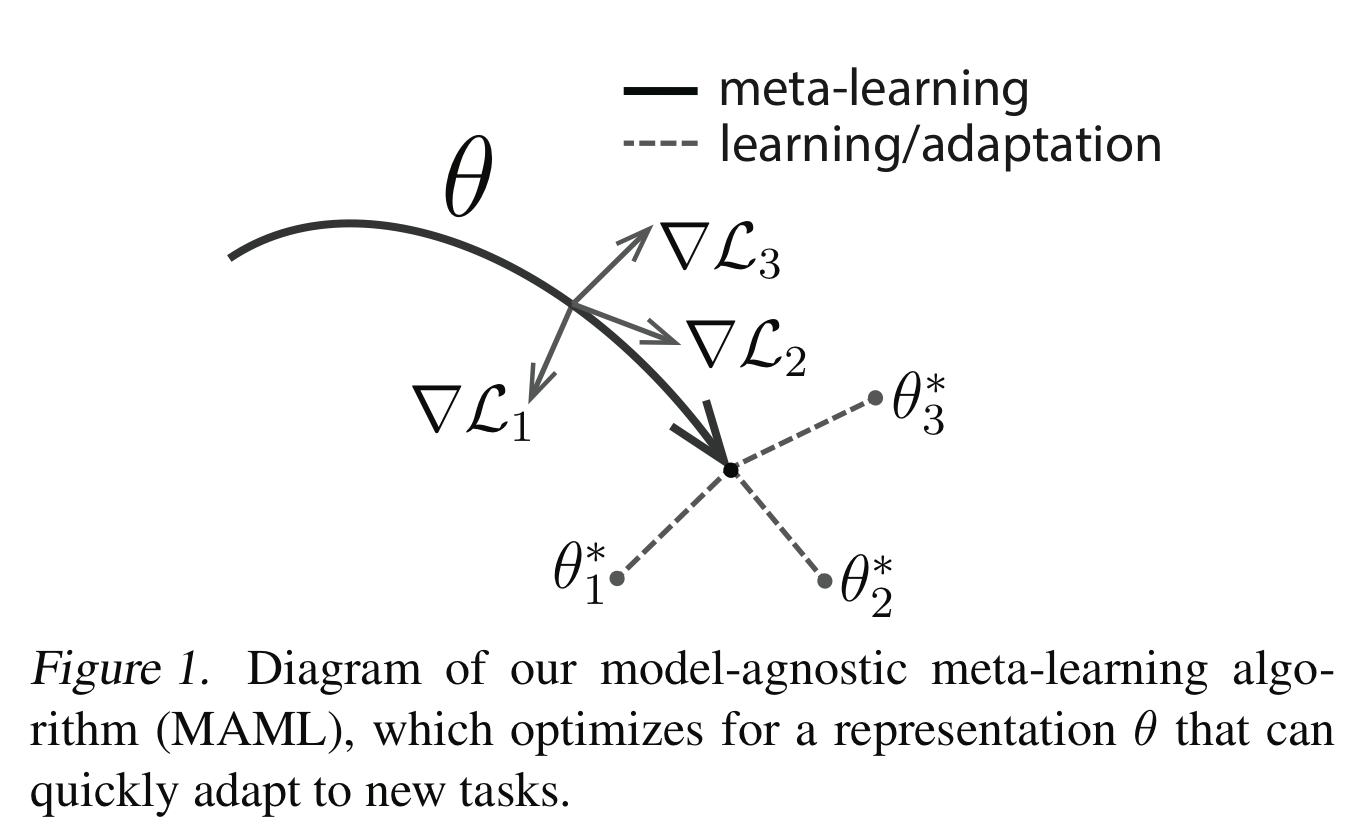
Model-Agnostic Meta-Learning (MAML) tries to find an initial parameter vector ? that can be quickly adapted via meta-task gradients to task-specific optimal parameter vectors.
Related Documents
- See paper Model-Agnostic Meta-Learning for Fast Adaptation of Deep Networks for details.
Related Videos
Comments
-
-
I don't think I've ever wanted to pass a test this badly.
-

Reply