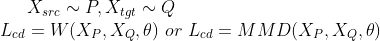1
1Problem Definition of Cross-Domain Recommendation
Cross-Domain Recommendation is getting more popular in recent years. There are many applications, including e-commence website, instant video streaming, etc. In this post we are sharing some experience when we are building a cross-domain recommendation system in local service e-commence recommendation scenario, a hybrid feeds recommendation service. We define 'domain' as group of categories of items that we are recommending to users. Local service recommendation deal with heterogeneous items from multiple domains, including local stores, restaurants, movie theaters, POI(point of interest) etc. They have common item-side features shared by many domains, and individual features owned by each domain as well. The objective of cross-domain recommendation is to train a ranking model : With a single output for all domains, or a multi-tasks model with multiple ranking outputs for each individual domains.
Approach
Let's denote as set of users and
as set of items. Suppose items can be devided into m different groups or domains,
.
Group m
have
unique items. For cross-domain recommendation, we are training a ranking model with a single output for all different items,
.
denotes the label {0,1} of dataset as whether user click the item or not.
Embedding & Mapping Approach
One common approach to deal with cross domain recommendation is embedding & mapping approach. The idea is very simple, which is to embed item features from multiple heterogeneous domains to common embedding space, and then use a single ranking function (usually a deep neural network) to learn this function. Let's denote as the feature from the i th domain for items
. And we learn a mapping function
to get the latent representation of item features in i-th domain. Finally, the loss function is design to minimize the decrepancy among multiple domain,
. The loss function is usually MSE(mean-squared error) loss.
Transfer learning approach
One drawback of the embedding & mapping approach is that sometimes the features space of each domain is so diverse, that mapping all items features with minimal MSE loss is not necessary, sometime will even hurt the prediction performance. Some experts propose to use different distribution metric to constrain the difference in latent representation of different domain, which generalize much better then the exact mapping. Common choices of distance metric including MMD(maximum mean discrepancy), KL divergence, Wasserstein Distance.
MMD(maximum mean discrepancy)
MMD is a distance metric in two-sample test problem, to measure if samples from two distribution and
are the same.
Suppose there are two dataset
and
, which follows different distribution
. There are m samples in dataset X and n samples in dataset Y. There are many functions to transform the original dataset X and Y to f(X) and f(Y). The idea of MMD is to find a function f to maximize the differences of mean value function between two expectation
and
. And when two distribution are identical, the distance measure is 0.
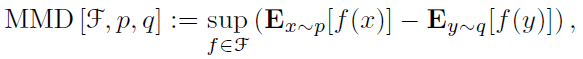
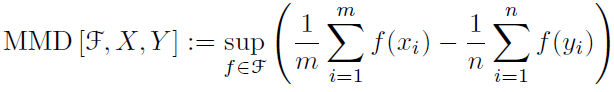
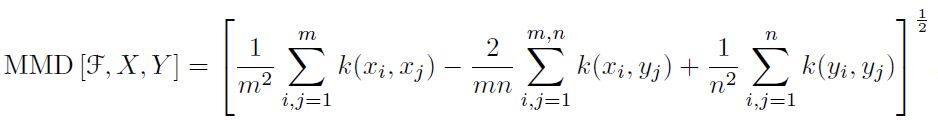
Wasserstein Distance
Wasserstein distance or (earth-mover distance) is popular with success application in Wasserstein GAN. Wasserstein distance is a distance measure
when solving the OT(Optimal Transport) problem, which is the cost to push distribution towards distribution
. Compared to KL divergence or JS divergence, Wasserstein distance of much smoother, especially when two distribution are note overlapped at all.
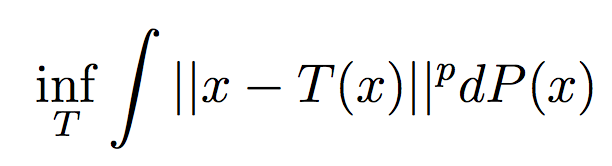
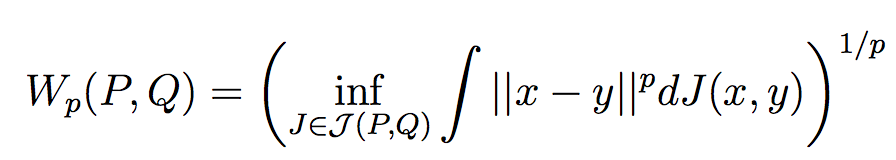
Cross domain layer
In the cross-domain recommendation, we devise a cross-domain layer to map original features from original source domain to target domain. Then we can learn a ranking function
.
as the cross-domain recommendation function. Then final loss function of cross-domain recommendation consists of two parts, the cross-entropy loss of recommendation tasks and the penalty of distance measure of different domains as :