X

OpenAI o1

#reasoning #math #science #code
6 Reviews
4.5

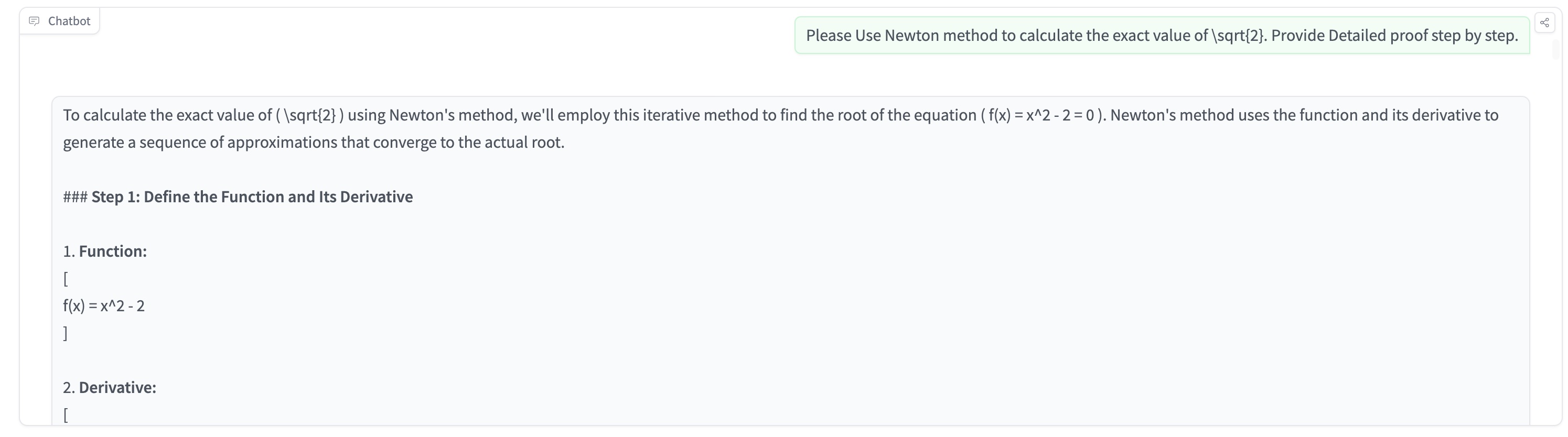
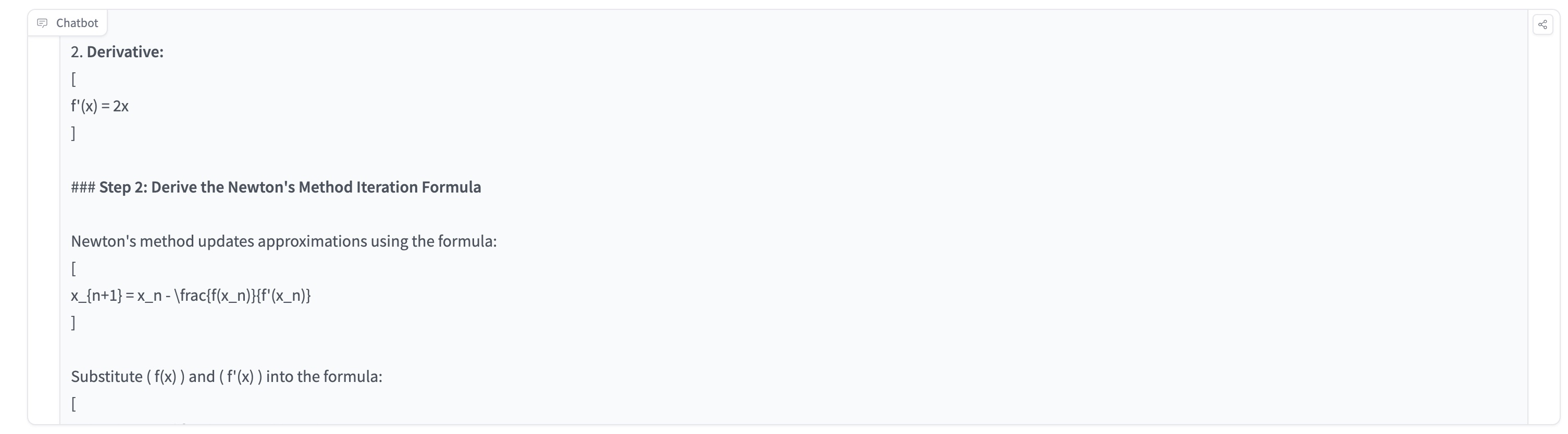
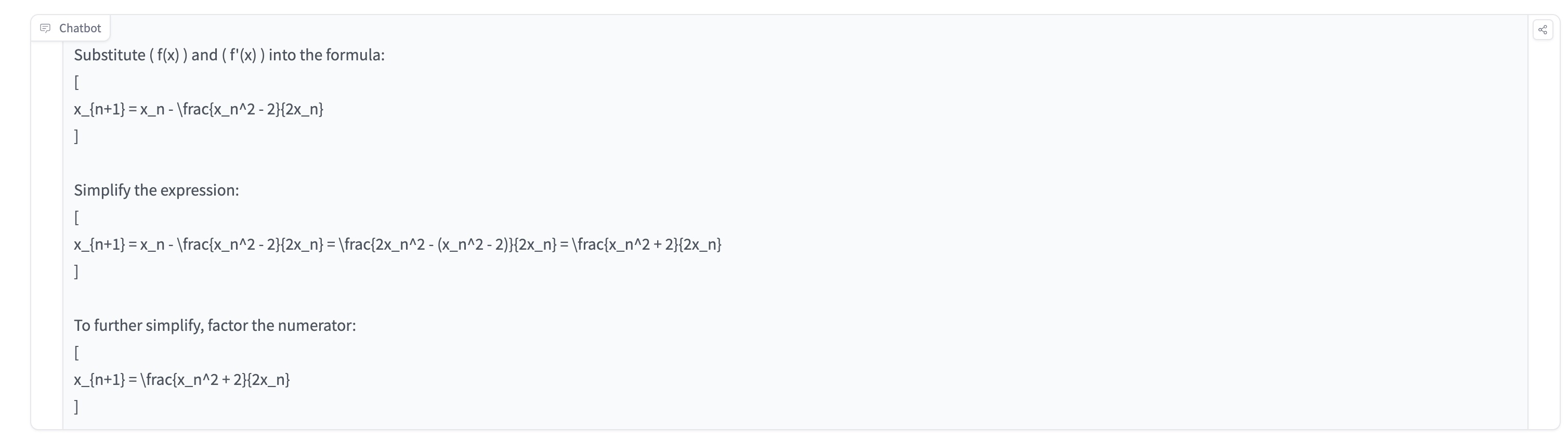
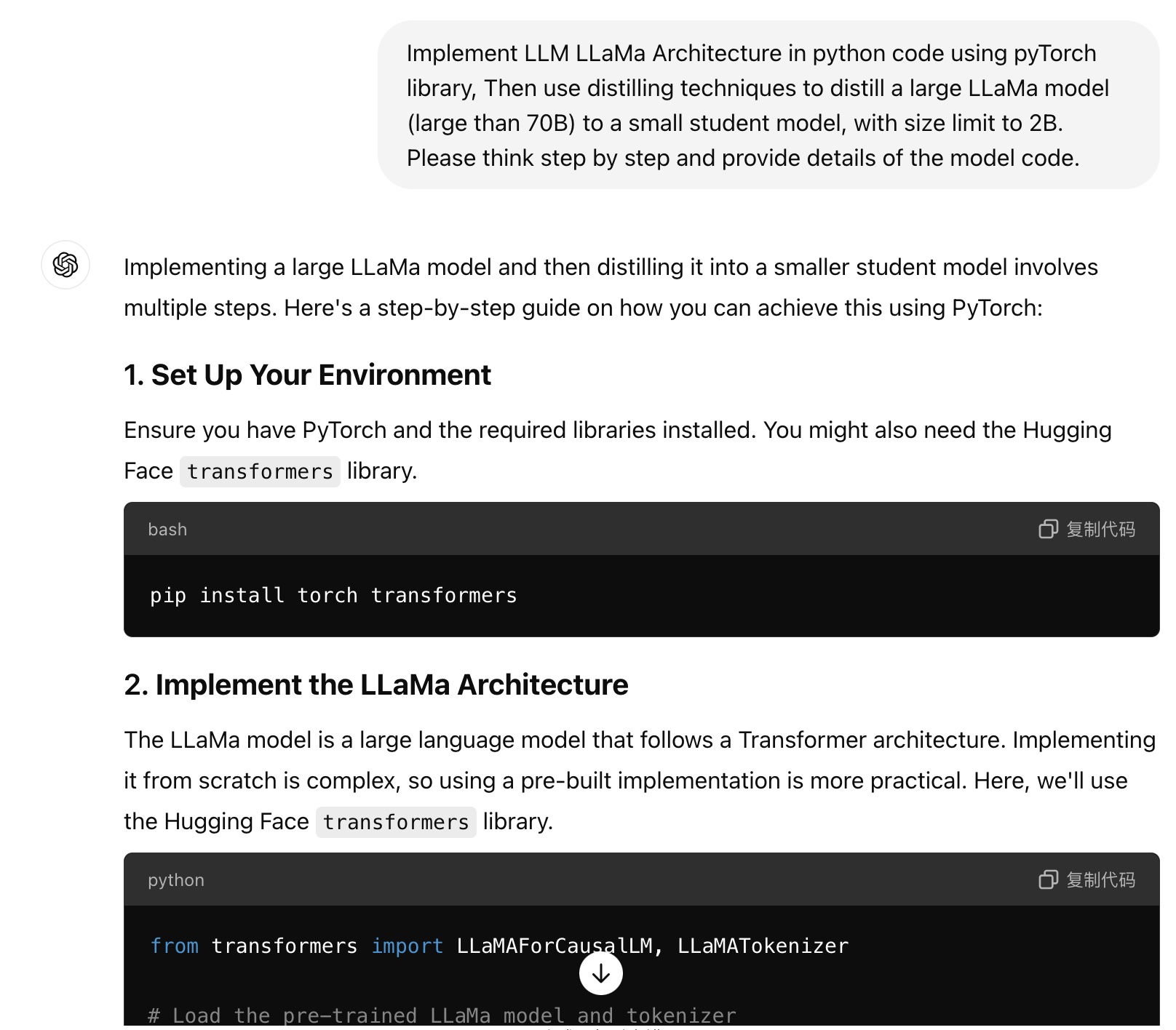
OpenAI just released a new series of reasoning models for solving hard problems such as science, coding, and math. It's said that o1 model performs similarly to PhD students on challenging benchmark tasks in physics, chemistry, and biology. We also found that it excels in math and coding. In a qualifying exam for the International Mathematics Olympiad (IMO), GPT-4o correctly solved only 13% of problems, while the reasoning model scored 83%. Their coding abilities were evaluated in contests and reached the 89th percentile in Codeforces competitions. Source: https://openai.com/index/introducing-openai-o1-preview/

Ratings

ALL
4.5
Correctness
4.8
Helpfulness
4.7
Interesting
3.3
Concise
3.0
Long Inference Time
3.0

Compare with Similar AI Apps

Use Cases

Prompts

1

Implement LLM LLaMa Architecture in python code using pyTorch library, Then use distilling techniques to distill a large LLaMa model (large than 70B) to a small student model, with size limit to 2B. Please think step by step and provide details of the model code.

2

Write front end code of the login and logout pages for H5 mobile application usage. Split the code in separate files for css, html, and js.

3

Please Use Newton method to calculate the exact value of \sqrt{2}. Provide Detailed proof step by step.

4

Let n be an even positive integer. Let p be a monic, real polynomial of degree 2n; that is to say, p(x)=x^{2n} + a_{2n-1}x^{2n-1} + ... + a_{1}x+ a_{0} for some real coefficients a_{0}, a_{1}, ..., a_{2n-1}. Suppose that p(1/k) = k^{2} for all integers k such as 1<=|k|<=n. Find all other real numbers x for which p(1/x)=x^2.

5

Can you provide proof of Riemann Hypothesis. Please think step by step.

6

Write a bash script that takes a matrix represented as a string with format '[1,2],[3,4],[5,6]' and prints the transpose in the same format.

Reviews

Tags

all math coding image video color consistency reasoning fantasy cartoon

  • M
    maththug 2024-09-18 12:22
    4.0
    Interesting:3,Helpfulness:4,Correctness:4
    Prompt: Can you provide proof of Riemann Hypothesis. Please think step by step.

    I asked OpenAI o1 the question to "Provide proof of Riemann Hypothesis" and think step by step. And here is the result. "It first mentioned that there is no known proof of the Riemann Hypothesis. However, I can outline some of the key ideas and approaches". Here are the detailed steps of OpenAI o1 models' response to "Riemann Hypothesis". Step-by-Step Overview of the Riemann Hypothesis 1. Understanding the Riemann Zeta Function 2. Critical Line and Zeros 3. Connection to Prime Numbers 4. Riemann's Original Approach 5. Analytic Continuation and Functional Equation: 6. Numerical Evidence: 7. Connections to Other Areas 8. Partial Results and Related Theorems 9. Approaches and Techniques 10. Current Status

    2
    0
    Follow
    Share

  • M
    MayZhou 2024-09-14 12:22
    4.0
    Interesting:3,Concise:3,Helpfulness:4,Correctness:5
    Prompt: Please Use Newton method to calculate the exact value of \sqrt{2}. Provide Detailed proof step by step.

    To test OpenAI o1 model's ability of graduate-level machine learning & math, I tried to ask OpenAI o1 to solve the problem of "Use Newton method to calculate the exact value of \sqrt{2}. Provide Detailed proof step by step." OpenAI o1 actually gives me a very long detailed step-by-step proof, which is much detailed and longer than GPT4o or GPT4o-mini. The complete response is very long and I just summarized the detailed steps of the reasoning here. Overall, I think OpenAI o1 can provide more accurate responses than previous GPT4o' answers. But the response usually is very long and there are a lot of top-down break-down, which makes the final result correct but sometimes hard to understand and follow. OpenAI o1 breaks down the machine learning math problem into these steps: ### Step 1: Define the Function and Its Derivative ### Step 2: Derive the Newton's Method Iteration Formula ### Step 3: Choose an Initial Approximation ### Step 4: Perform Iterations ### Step 5: Understanding the Result Each iteration yields a rational approximation that gets closer to ( \sqrt{2} ): - Iteration 1: ( x_1 = \dfrac{3}{2} = 1.5 ) - Iteration 2: ( x_2 = \dfrac{17}{12} \approx 1.4167 ) - Iteration 3: ( x_3 = \dfrac{577}{408} \approx 1.41422 ) - Iteration 4: ( x_4 = \dfrac{667,217}{471,632} \approx 1.41421 ) ### Conclusion Using Newton's method with the function ( f(x) = x^2 - 2 ) and starting approximation ( x_0 = 1 ), we generate a sequence ( { x_n } ) defined by: [ x_{n+1} = \frac{1}{2} \left( x_n + \frac{2}{x_n} \right) ] This sequence converges to ( \sqrt{2} ) as ( n ) approaches infinity. ### Final Answer By applying Newton's method to the equation ( x^2 - 2 = 0 ), we find that ( \sqrt{2} ) is the limit of the sequence: [ x_{n+1} = \dfrac{1}{2} \left( x_n + \dfrac{2}{x_n} \right) ] Starting from ( x_0 = 1 ), each iteration gives a rational approximation of ( \sqrt{2} ). Although we cannot express ( \sqrt{2} ) exactly using Newton's method (since it's irrational), the method provides increasingly accurate approximations.

    1
    0
    Follow
    Share

  • X
    xiaolei98 2024-09-13 12:18
    5.0
    Interesting:5,Helpfulness:5,Correctness:5
    Prompt: Implement LLM LLaMa Architecture in python code using pyTorch library, Then use distilling techniques to distill a large LLaMa model (large than 70B) to a small student model, with size limit to 2B. Please think step by step and provide details of the model code.

    I asked the OpenAI o1 model to implement the LLaMa Architecture LLM in python code using pytorch with a distill function. The overall response is excellent. It breaks down the tasks into a few steps, including : 1. Set Up Your Environment 2. Implement the LLaMa Architecture 3. Prepare the Distillation Process And as for the code it self, it consists of a few sections, including: Load the large LLaMa model and tokenizer. Prepare a smaller student model for distillation. Define a custom distillation loss function. Create a custom dataset for training. Set up a trainer with the distillation loss function. Train the student model using the teacher model. I actually examined the distill loss coding, which is the KL Divergence between the student logits and the teacher logits. The results are correct. """ loss = nn.functional.kl_div(student_probs, teacher_probs, reduction='batchmean') """

    0
    0
    Follow
    Share

  • X
    xiaolei98 2024-09-13 12:16
    4.0
    Interesting:3,Helpfulness:5,Correctness:5
    Prompt: Write front end code of the login and logout pages for H5 mobile application usage. Split the code in separate files for css, html, and js.

    I used the OpenAI o1 preview model to implement the frontend code of login and logout function of H5 mobile application and separate css, html and js code into separate files. The model's response to the front end code generation task is very helpful. And I actually copy and paste the code into a separate folder and tried it myself. The website front end is shown in the attached images. It is working to some extend, except that the CSS file is a little bit strange. The o1 model generates the code and also gives these explanations, including: index.html: Contains the structure of the login and logout pages. styles.css: Provides the styling for the pages to make them mobile-friendly. scripts.js: Handles the login and logout functionality. It uses localStorage to persist the logged-in state.

    0
    0
    Follow
    Share

  • A
    ai4science03 2024-09-13 08:54
    5.0
    Interesting:3,Helpfulness:5,Long Inference Time:3,Correctness:5
    Prompt: Write a bash script that takes a matrix represented as a string with format '[1,2],[3,4],[5,6]' and prints the transpose in the same format.

    OpenAI o1 coding ability reviews of reasoning with LLM. In their official website, the prompt for OpenAI o1 is to "takes a matrix represented as a string with format '[1,2],[3,4],[5,6]' and prints the transpose in the same format."After comparing the results of o1 with GPT4o and the final scripts are actually much longer, o1 results have 70 lines of scripts but the GPT4o has only 31 lines of code. The key difference is how to "Build output string". Source: https://openai.com/index/learning-to-reason-with-llms/

    0
    0
    Follow
    Share

  • A
    ai4science03 2024-09-13 08:44
    5.0
    Interesting:3,Helpfulness:5,Correctness:5
    Prompt: Let n be an even positive integer. Let p be a monic, real polynomial of degree 2n; that is to say, p(x)=x^{2n} + a_{2n-1}x^{2n-1} + ... + a_{1}x+ a_{0} for some real coefficients a_{0}, a_{1}, ..., a_{2n-1}. Suppose that p(1/k) = k^{2} for all integers k such as 1<=|k|<=n. Find all other real numbers x for which p(1/x)=x^2.

    Finally, OpenAI released o1 mdoel with stronger reasoning ability. And I looked through the detailed comparison of a math solving results on their website and the comparison between GPT4o vs OpenAI o1-preview on this Algebra problem. For the math question as the in the prompt, o1 uses a chain of thought when attempting to solve a problem, which is similar to how a human may think for a long time before responding to a difficult question. o1 response actually break down the question into a few steps: "Understanding the Given Information", "Defining a New Polynomial", "Properties of q(x)", "Constructing s(x)", "Matching Coefficients". Finding Additional Solutions and finally reaching Conclusion. The additional real numbers x satisfying p(1/x) = x^{2} are x=\frac{1}{n!} or -\frac{1}{n!}. Overall, the reasoning ability is quite complex compared to previous version, so it's helpful and the answers are correct.

    1
    0
    Follow
    Share

Write Your Review

Detailed Ratings

ALL
Correctness
Helpfulness
Interesting
Upload Pictures and Videos